Home » Mohammad Yahyavi

Mohammad Yahyavi

Position: PhD Student

Research Areas:Condensed Matter Physics, Quantum Mechanics, Statistical Mechanics, Computational Materials Science, Disordered systems, Molecular Dynamics Simulation, and Nonlinear Dynamics.

Research Projects:

We construct a topological one-dimensional ladder model following the steps which lead to the Kane-Mele model in two dimensions. Starting with a Creutz ladder we modify it so that the gap closure points can occur at either $k = \pi / 2$  or $-\pi/2$ . We then couple two such models, one for each spin channel, in such a way that time-reversal invariance is restored. We also add a Rashba spin-orbit coupling term. The model falls in the CII symmetry class. We derive the relevant $2\mathbb{Z}$  topological index, calculate the phase diagram and demonstrate the existence of edge states. We also give the thermodynamic derivation (Středa-Widom) of the quantum spin Hall conductance. Approximate implementation of this result indicates that this quantity is sensitive to the topological behavior of the model.
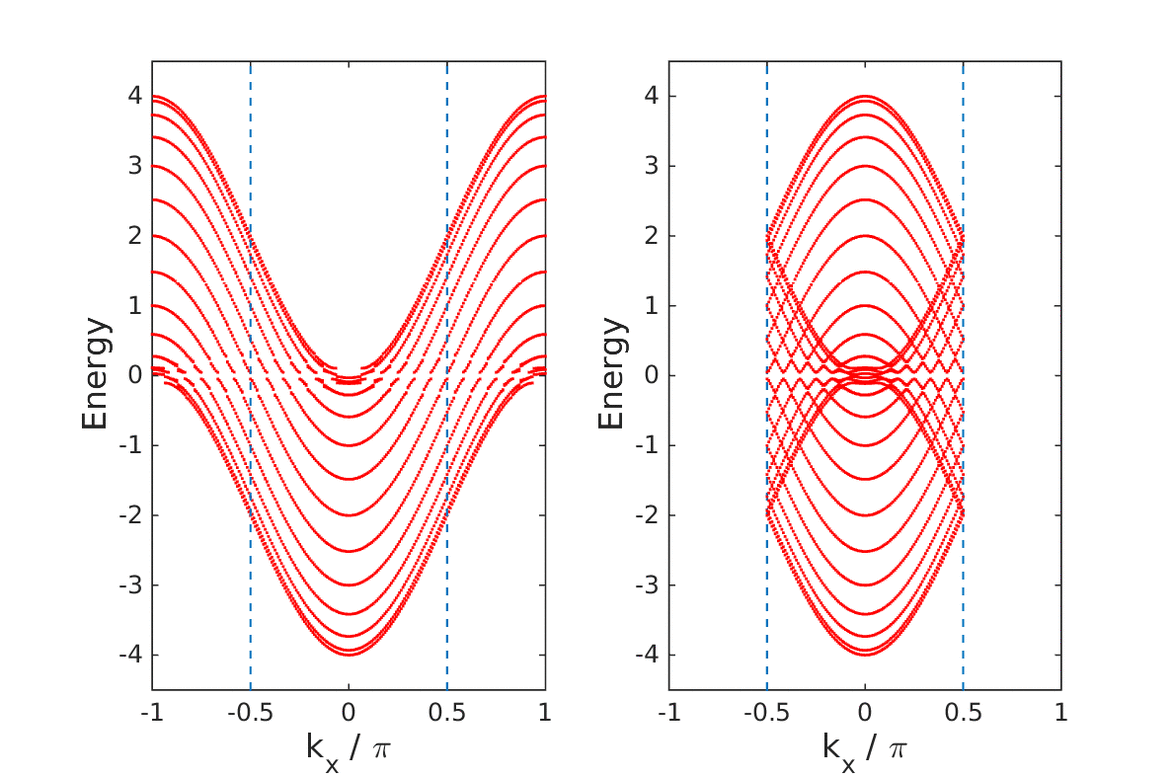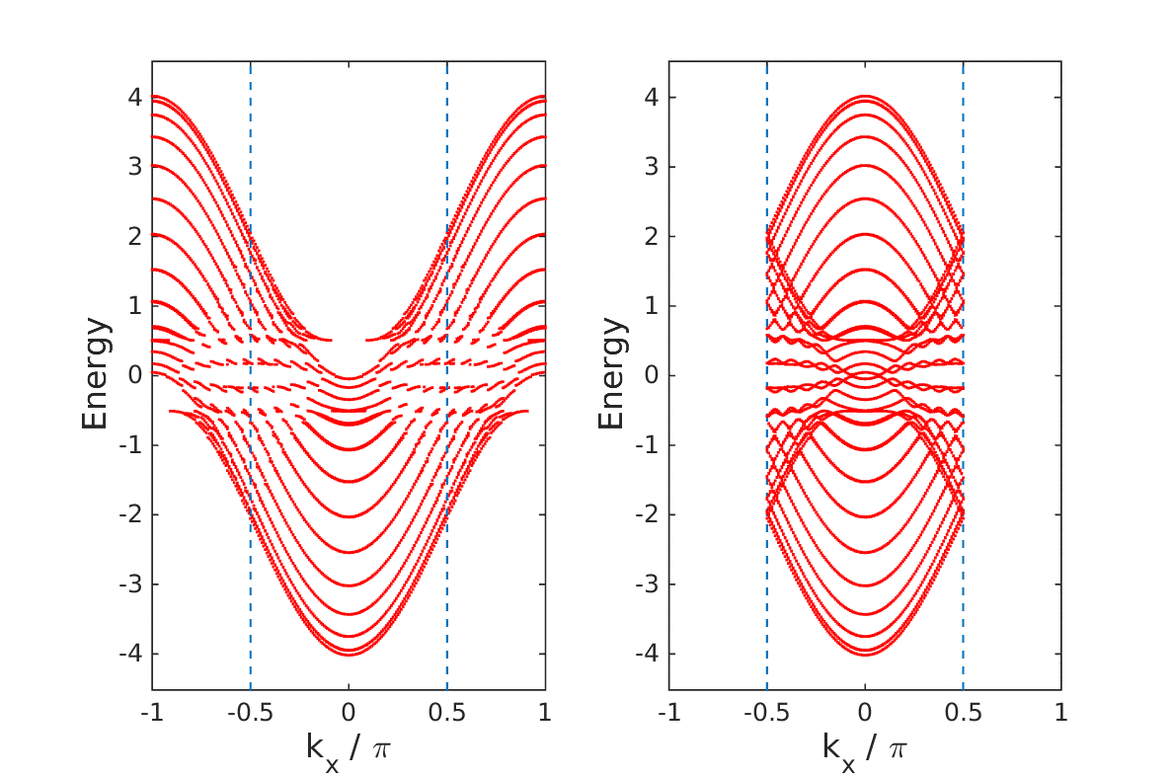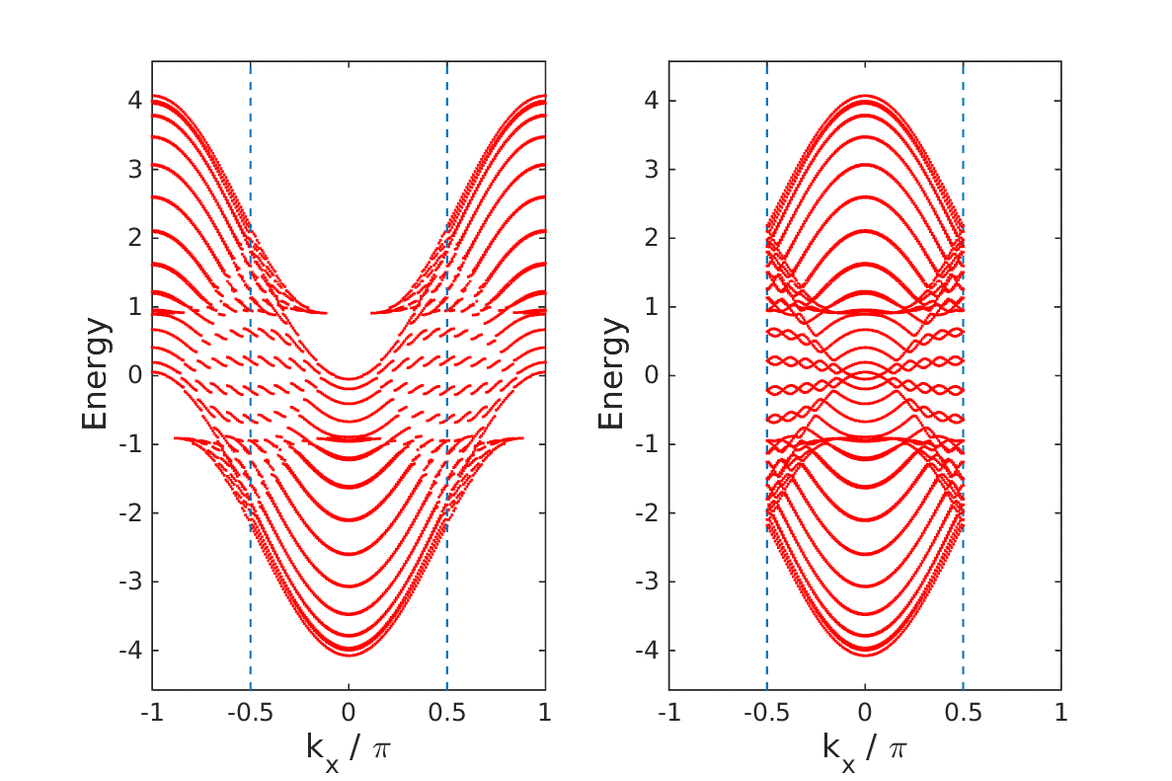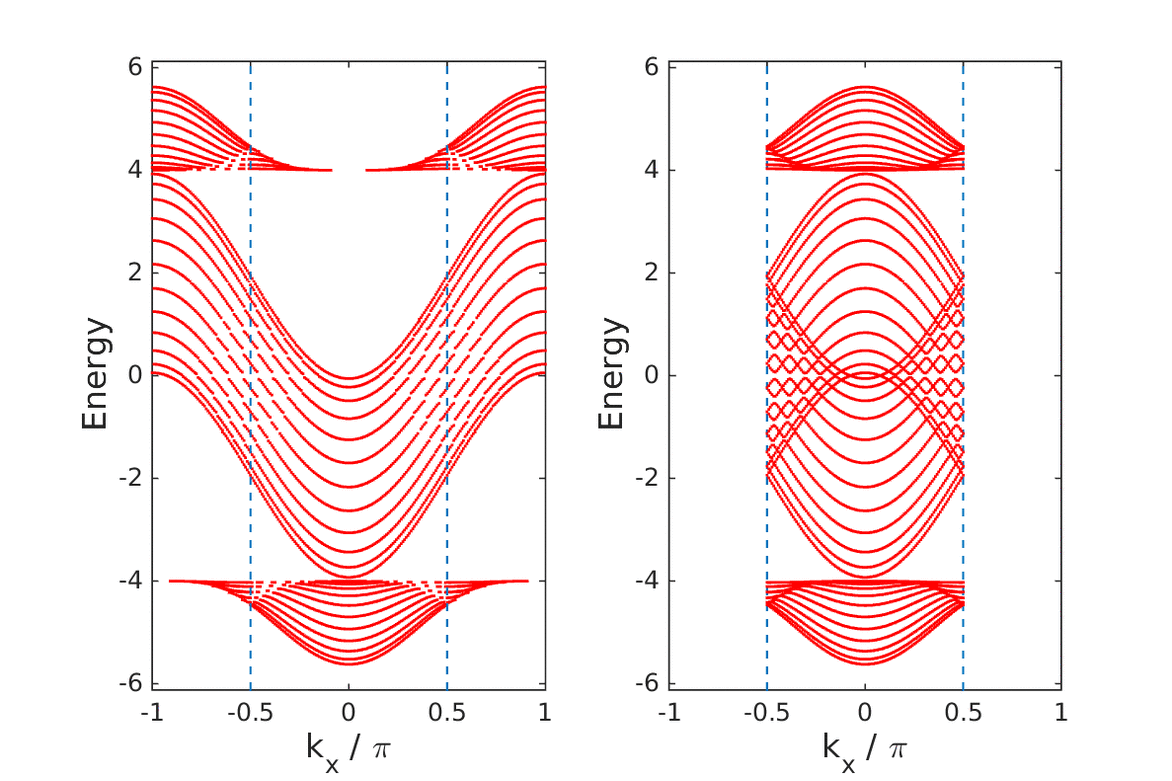
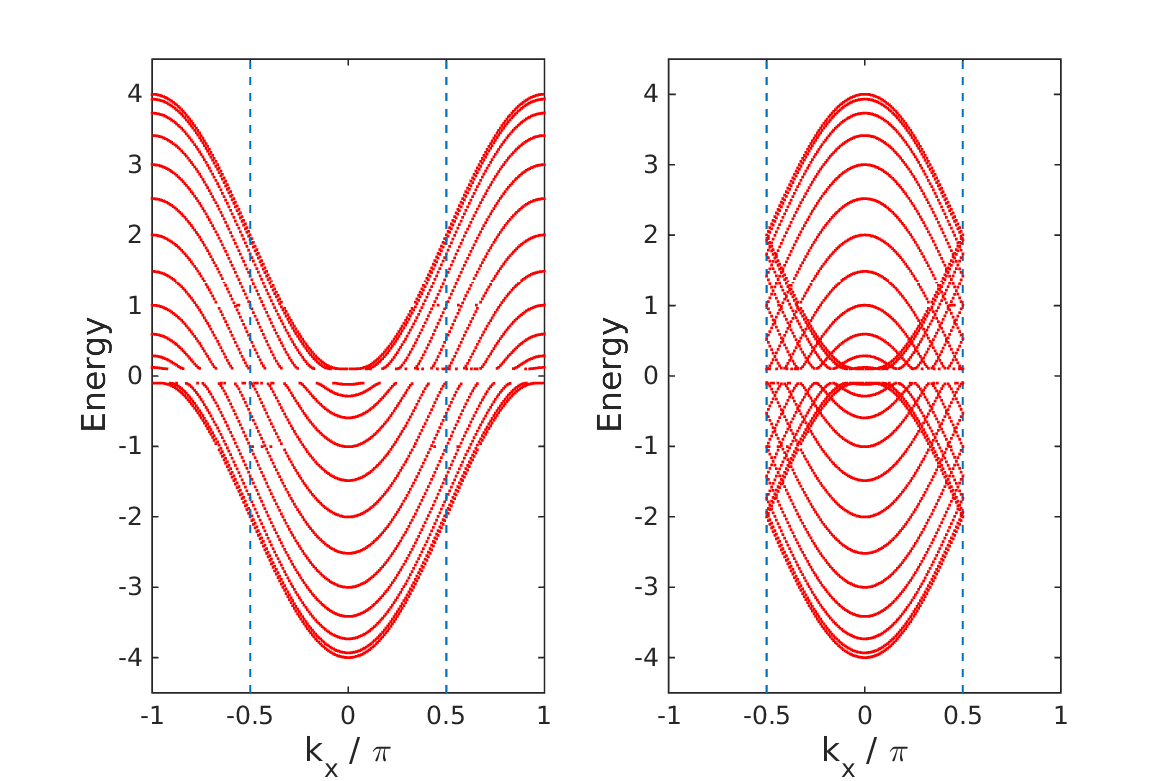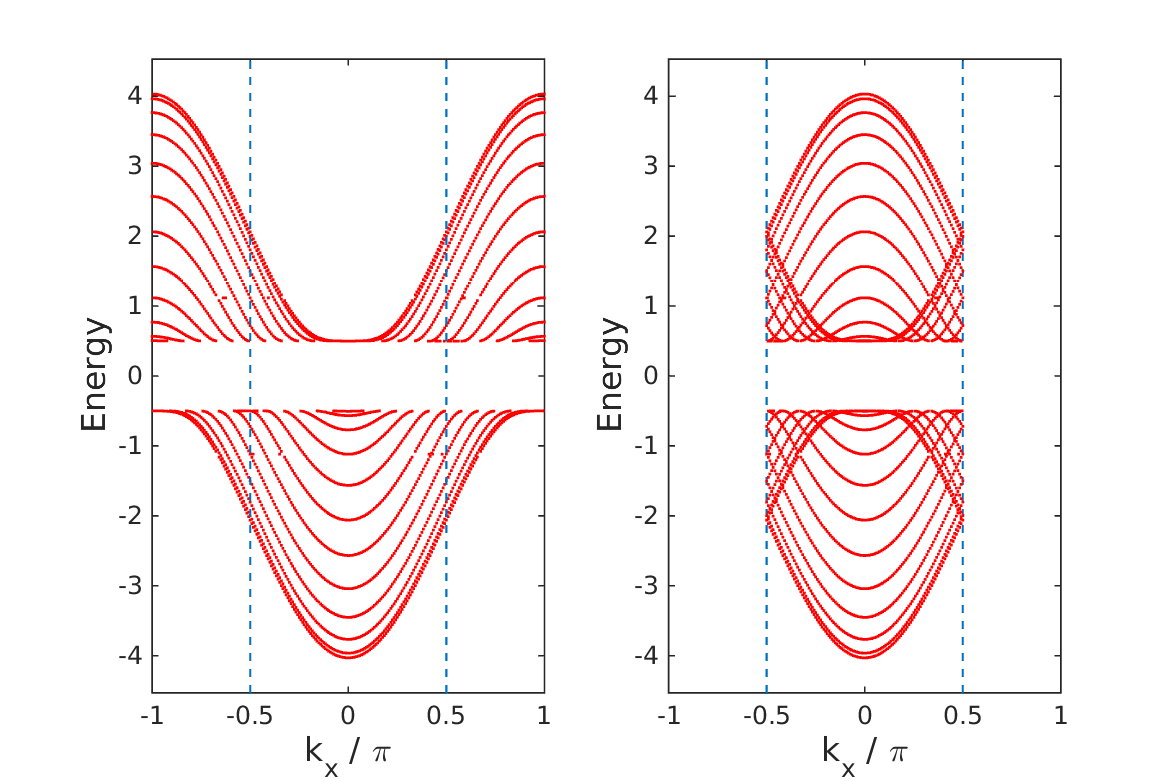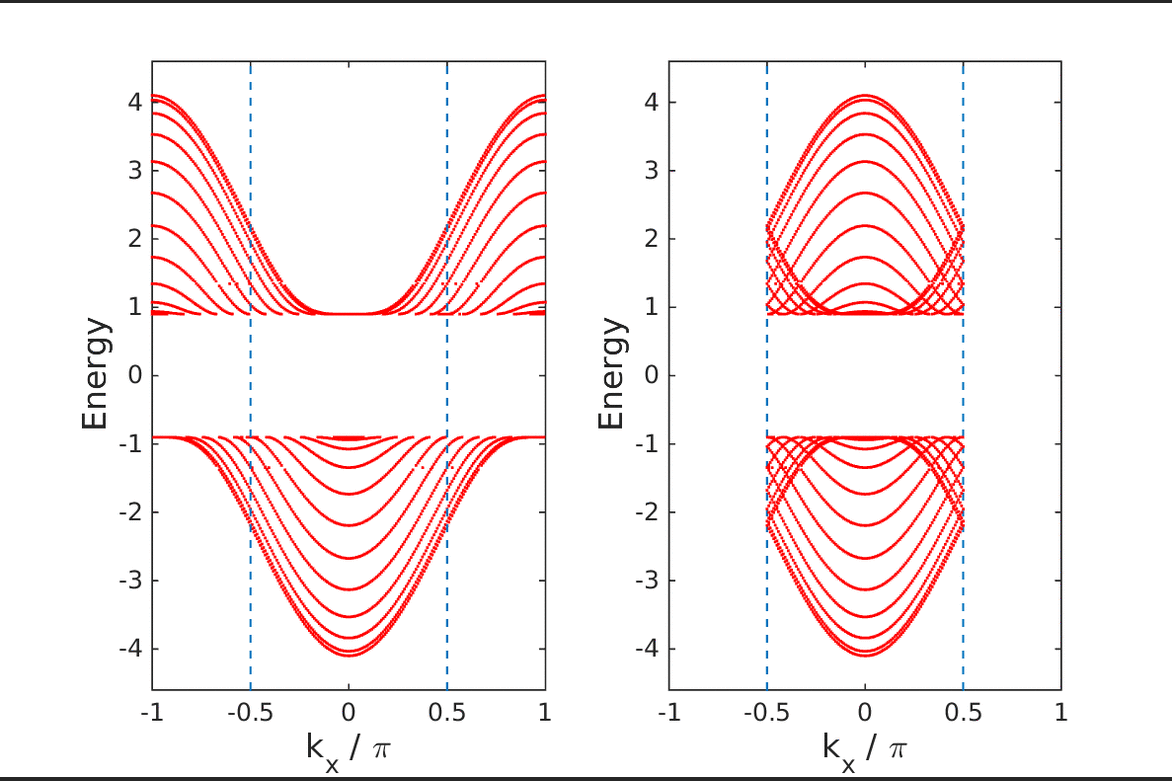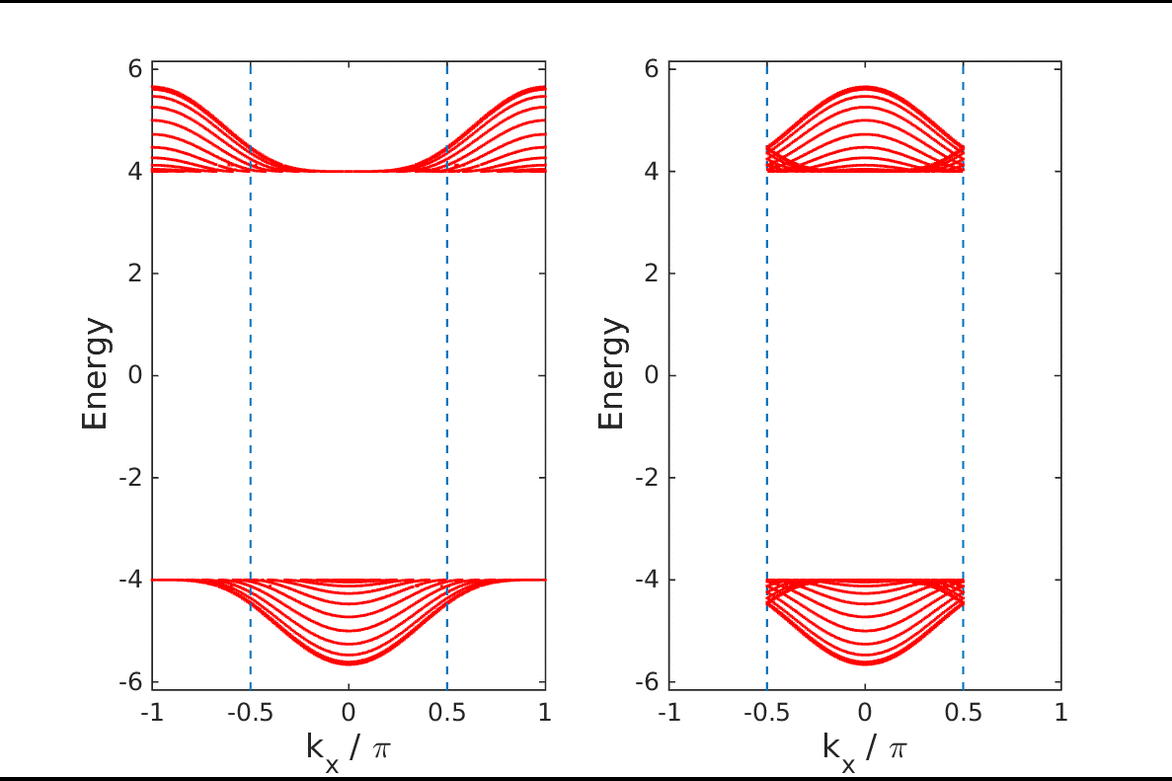
We calculate the gauge-invariant cumulants (and moments) associated with the Zak phase in the Rice-Mele model. We reconstruct the underlying probability distribution by maximizing the information entropy and applying the moments as constraints. When the Wannier functions are localized within one unit cell, the probability distribution so obtained corresponds to that of the Wannier function. We show that in the fully dimerized limit the magnitudes of the moments are all equal. In this limit, if the on-site interaction is decreased towards zero, the distribution shifts towards the midpoint of the unit cell, but the overall shape of the distribution remains the same. Away from this limit, if alternate hoppings are finite and the on-site interaction is decreased, the distribution also shifts towards the midpoint of the unit cell, but it does this by changing shape, by becoming asymmetric around the maximum, and by shifting.
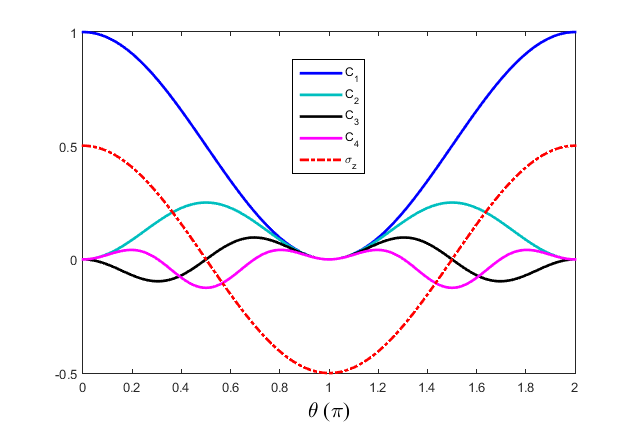
An expansion, similar to the cumulant expansion in probability theory, is carried out for the Bargmann invariant, which is the quantity from which the Berry phase can be derived. The derivation shows that the first term in the expansion corresponds to the Berry phase itself, the higher order terms can be interpreted as the associated cumulants; spread, skew, kurtosis, etc. The gauge invariance of all of these quantities is also demonstrated.

Cumulants of a spin-1/2 particle in a precessing field
It was recently shown that the transport coefficient of ideal conduction, the Drude weight, can be expressed in terms of a topological invariant. This suggests that an interface between an ideal conductor and an insulator, across which the topological invariant abruptly changes its value, should exhibit topological edge states. 

2015 poster

Topological aspects of ideal conduction (pdf) [poster]

Selected Publications:

Enhanced charge transport at the ideal conductor-insulator interface
M. Yahyavi , Balázs Hetényi
———————————————————————————————-

Extended Creutz ladder with spin-orbit coupling: A one-dimensional analog of the Kane-Mele model
S. Gholizadeh, M. Yahyavi, B Hetényi
EPL, 122 27001, (2018).

Topological insulation in a ladder model with particle-hole and reflection symmetries
B Hetényi, M. Yahyavi
J. Phys.: Condens. Matter 30 10LT01, (2018).

Reconstruction of the polarization distribution of the Rice-Mele model
M. Yahyavi, B Hetényi
Physical Review A 95 (6), 062104

Cumulants associated with geometric phases
B. Hetényi, M. Yahyavi
EPL (Europhysics Letters) 105 (4), 40005.

Effect of magnetic field on the radial pulsations of a gas bubble in a non-Newtonian fluid
S. Behnia, F. Mobadersani, M. Yahyavi, A. Rezavand, N. Hoesinpour, A. Ezzat
Chaos, Solitons & Fractals 78, 194-204.

Intelligent controlling microbubble radial oscillations by using Slave-Master Feedback control
S. Behnia, M. Yahyavi, F. Mobadersani
Applied Mathematics and Computation 245, 404-415.

Chaotic behavior of gas bubble in non-Newtonian fluid: a numerical study
S. Behnia, F. Mobadersani, M. Yahyavi, A. Rezavand
Nonlinear Dynamics 74 (3), 559-570.

Observations on the dynamics of bubble cluster in an ultrasonic field
S. Behnia, H. Zahir, M. Yahyavi, A. Barzegar, F. Mobadersani
Nonlinear Dynamics 72 (3), 561-574.

Characterization of intermittency in hierarchy of chaotic maps with invariant measure
S. Behnia, M. Yahyavi
Journal of the Physical Society of Japan 81 (12), 124008.

Generation of SWAP gate between two remote cavities via an optical fiber by adiabatic passage
L. Molouki, M. Yahyavi, P. Esmaili, E. Talebian
European Physical Journal Plus 127, 134.