The central aim of our research is to gain knowledge about physical phenomena which occur in condensed matter systems. To achieve this we rely on the tools of many-body physics. Currently, we are investigating whether conducting states of the topological kind exist at an interface between an ideal conductor and an insulator. We are also developing a variational Monte Carlo technique for lattice models, which we are applying to the bosonic Hubbard models in various dimensions. Another ongoing project is the description of transport (conduction, superconductivity, and superfluidity) based on the total momentum and related quantities. We are also investigating generalizations of the magnetic translation group.
We calculate the gauge-invariant cumulants (and moments) associated with the Zak phase in the Rice-Mele model. We reconstruct the underlying probability distribution by maximizing the information entropy and applying the moments as constraints. When the Wannier functions are localized within one unit cell, the probability distribution so obtained corresponds to that of the Wannier function. We show that in the fully dimerized limit the magnitudes of the moments are all equal. In this limit, if the on-site interaction is decreased towards zero, the distribution shifts towards the midpoint of the unit cell, but the overall shape of the distribution remains the same. Away from this limit, if alternate hoppings are finite and the on-site interaction is decreased, the distribution also shifts towards the midpoint of the unit cell, but it does this by changing shape, by becoming asymmetric around the maximum, and by shifting.
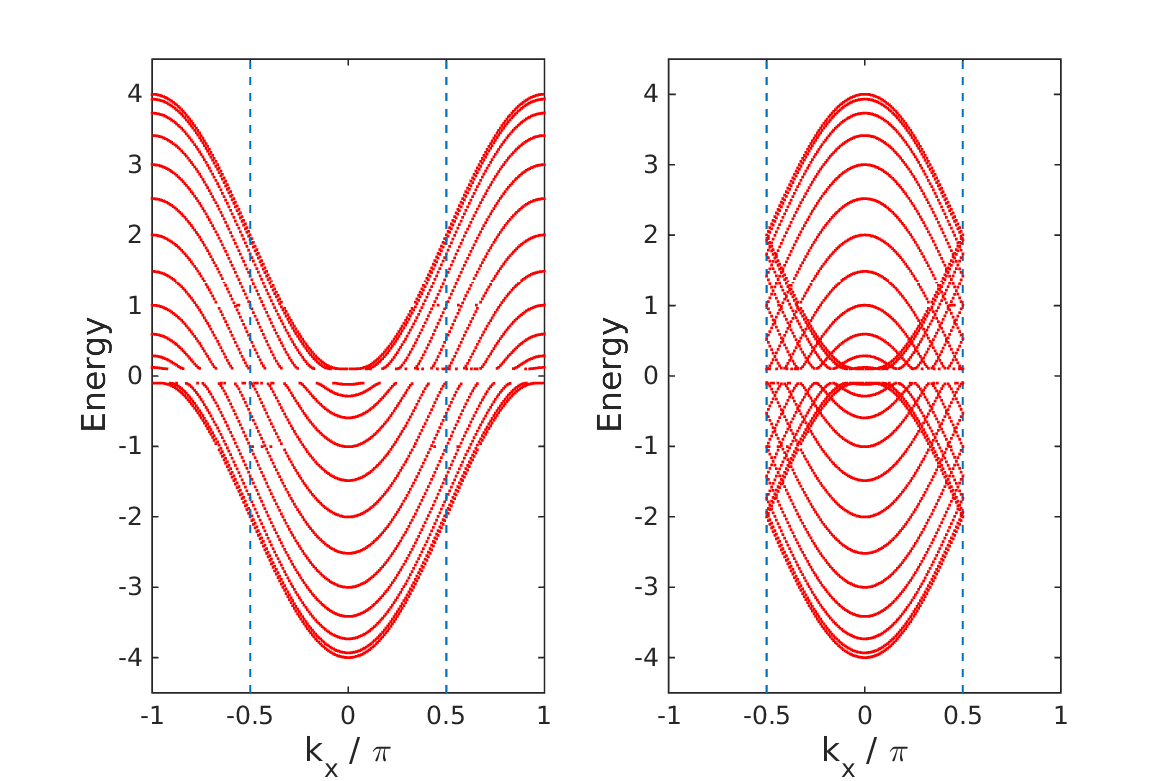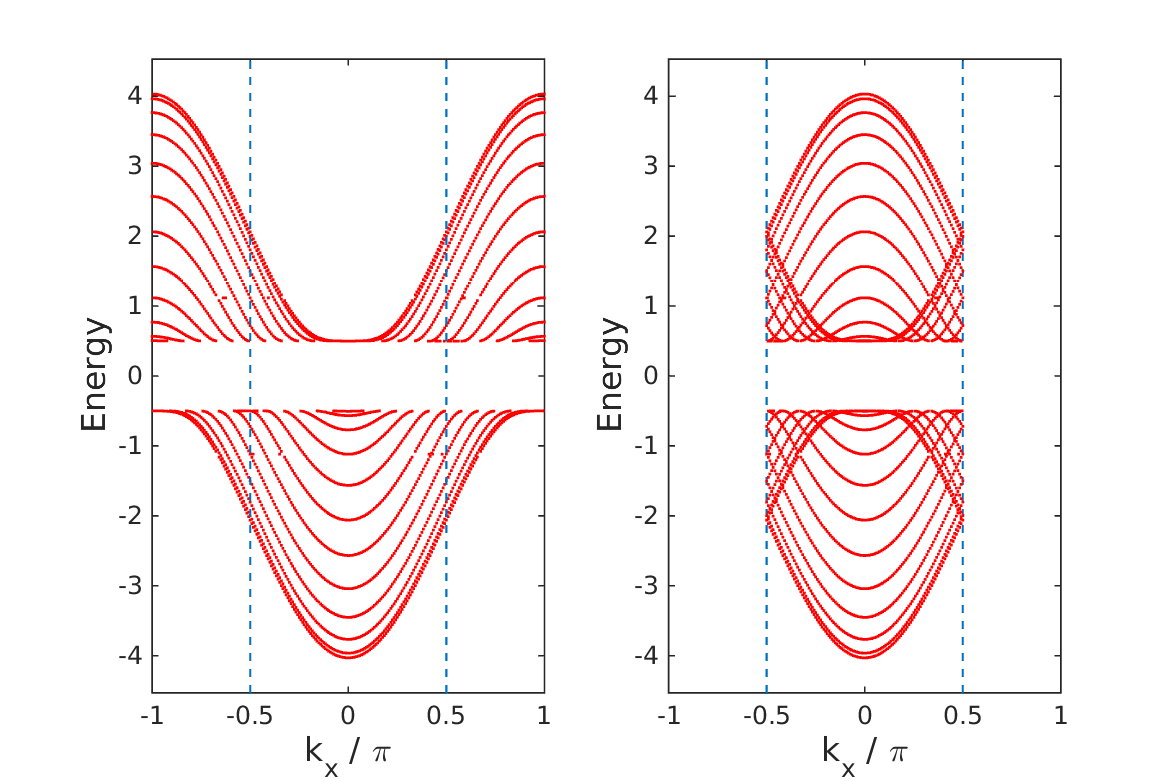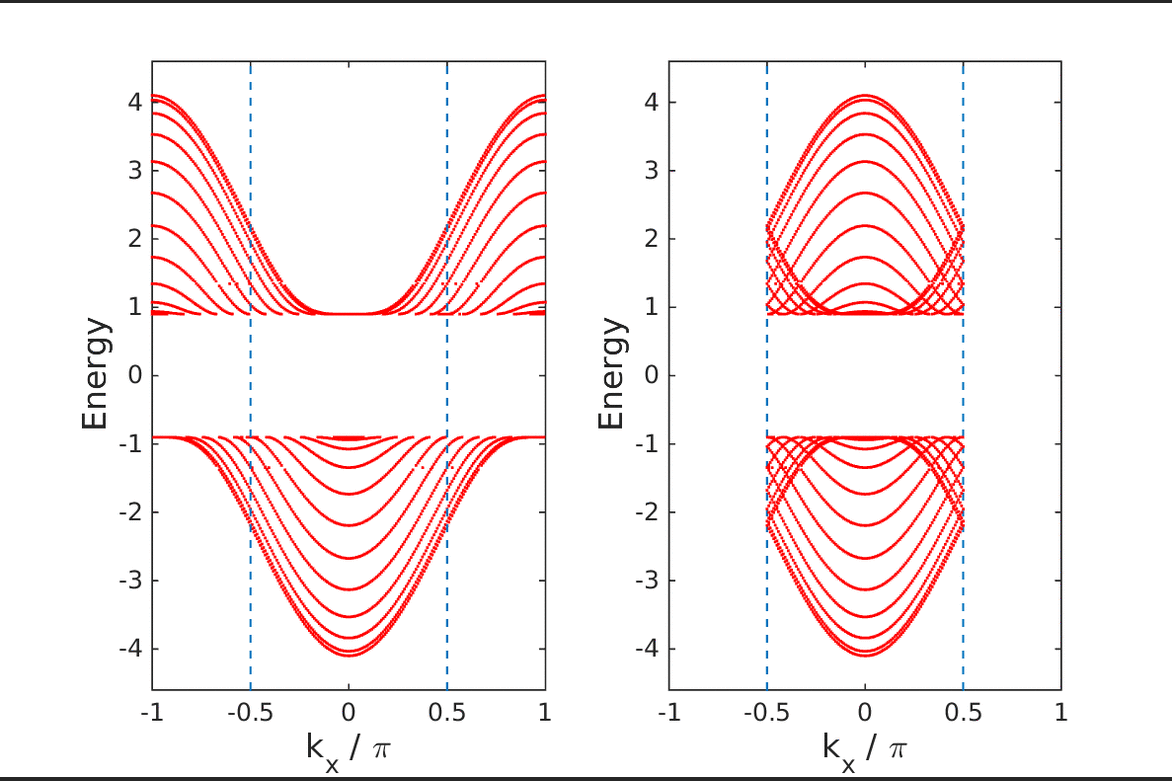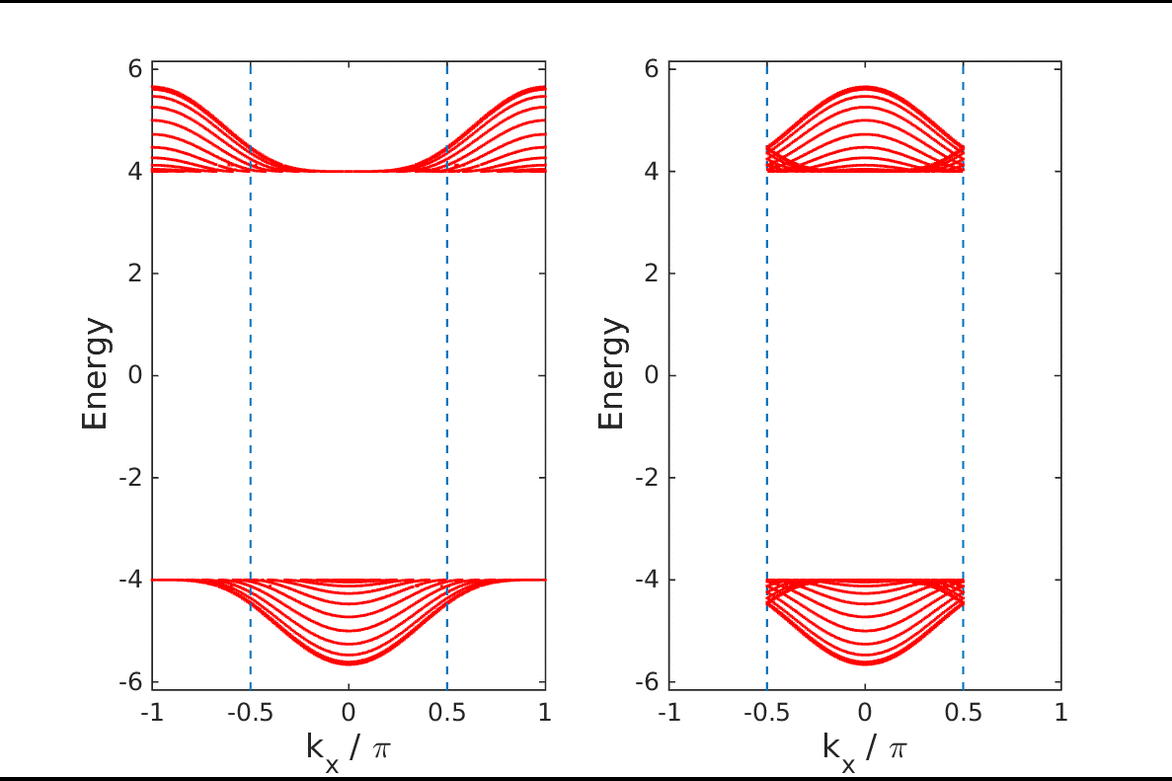
- Enhanced charge transport at the ideal conductor-insulator interface
It was recently shown that the transport coefficient of ideal conduction, the Drude weight, can be expressed in terms of a topological invariant. This suggests that an interface between an ideal conductor and an insulator, across which the topological invariant abruptly changes its value, should exhibit topological edge states.
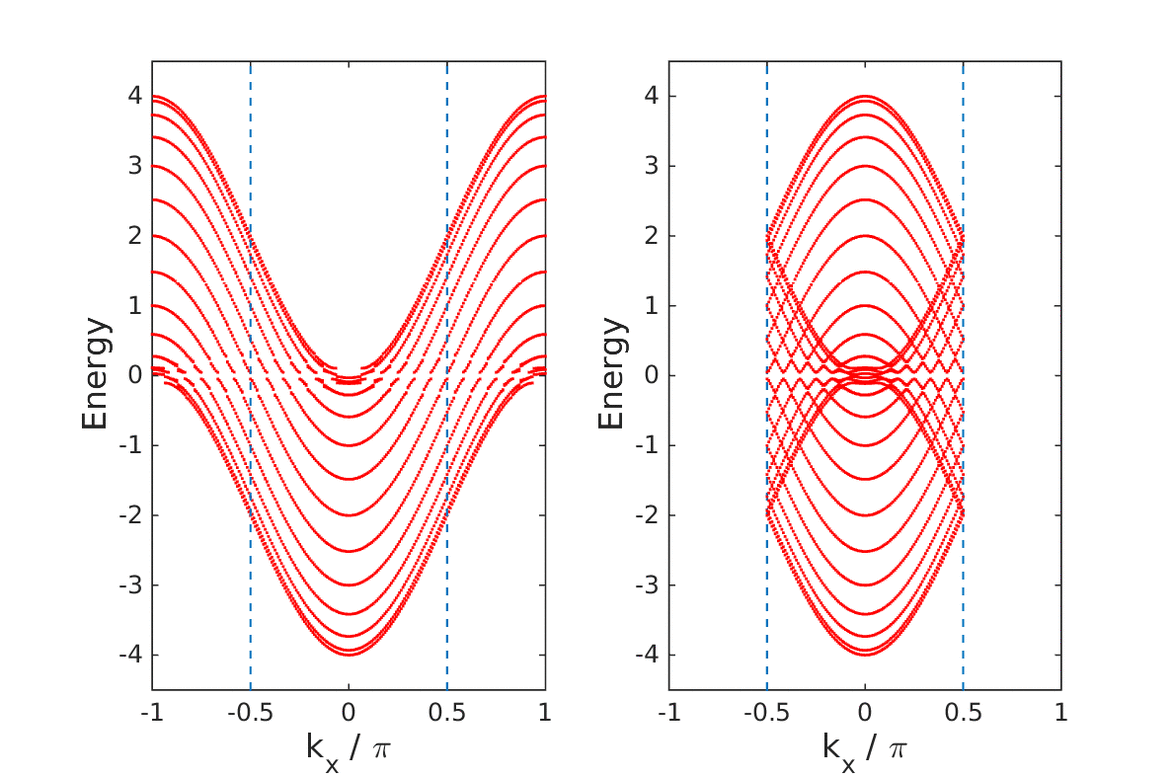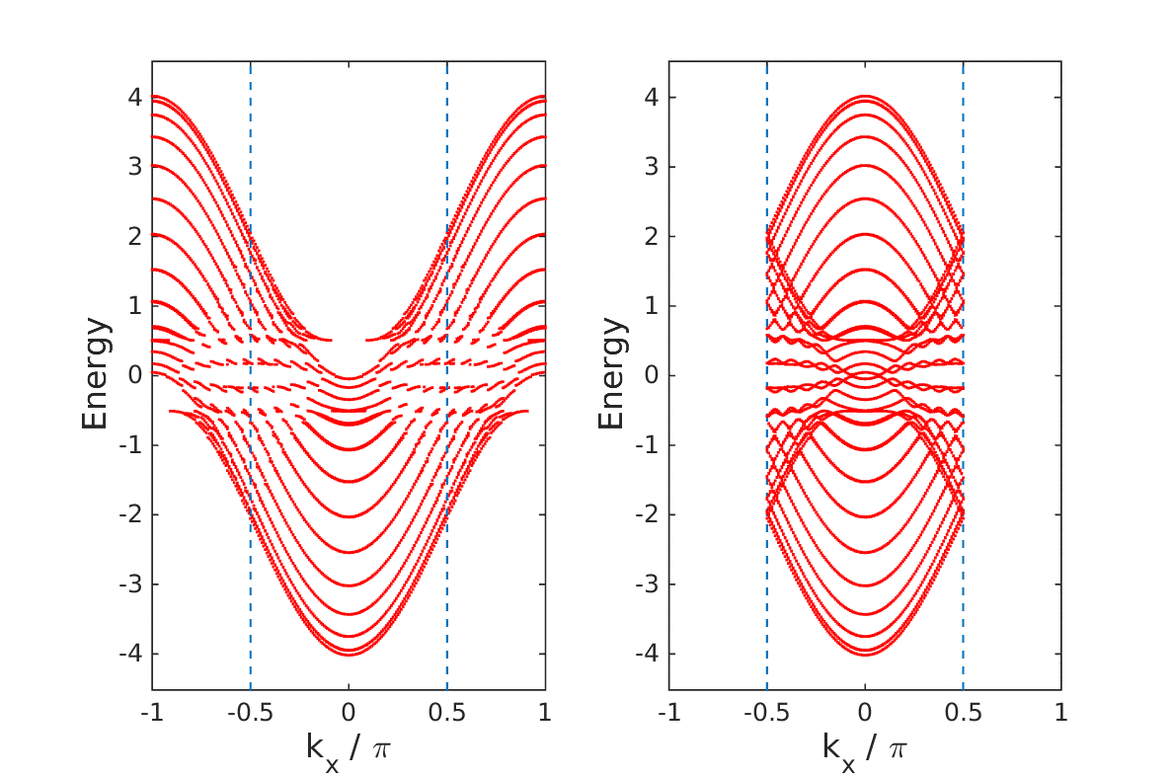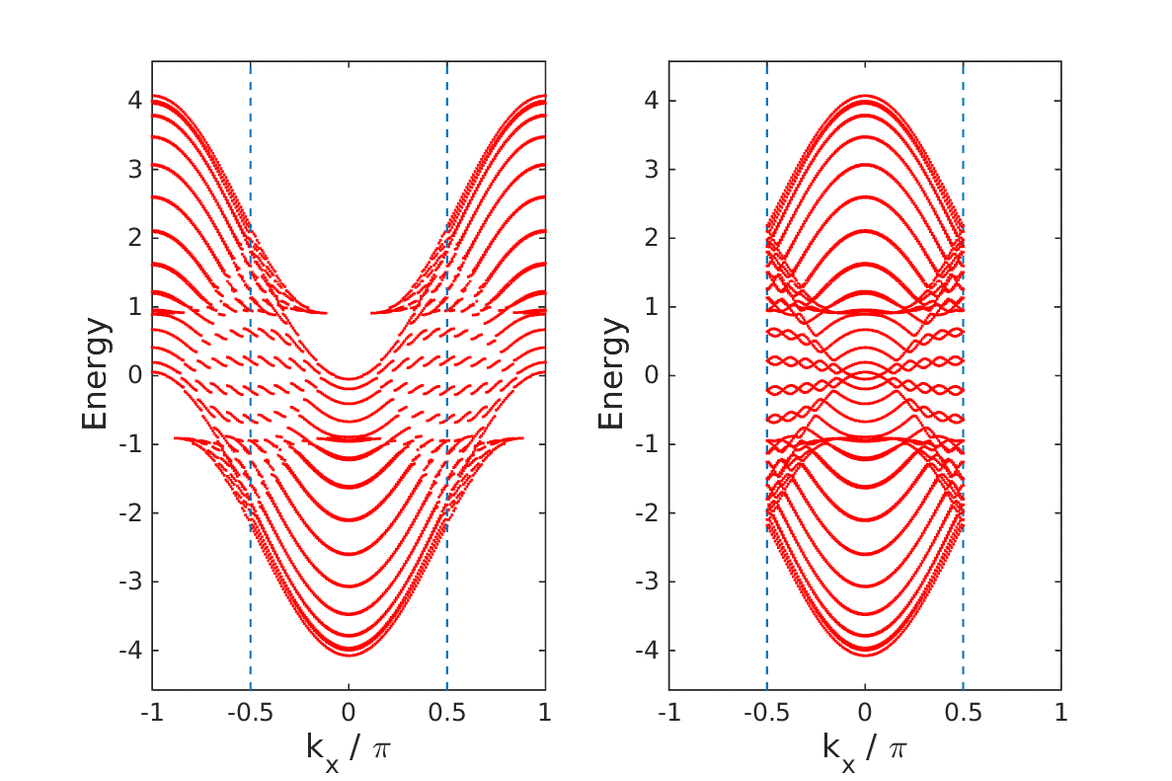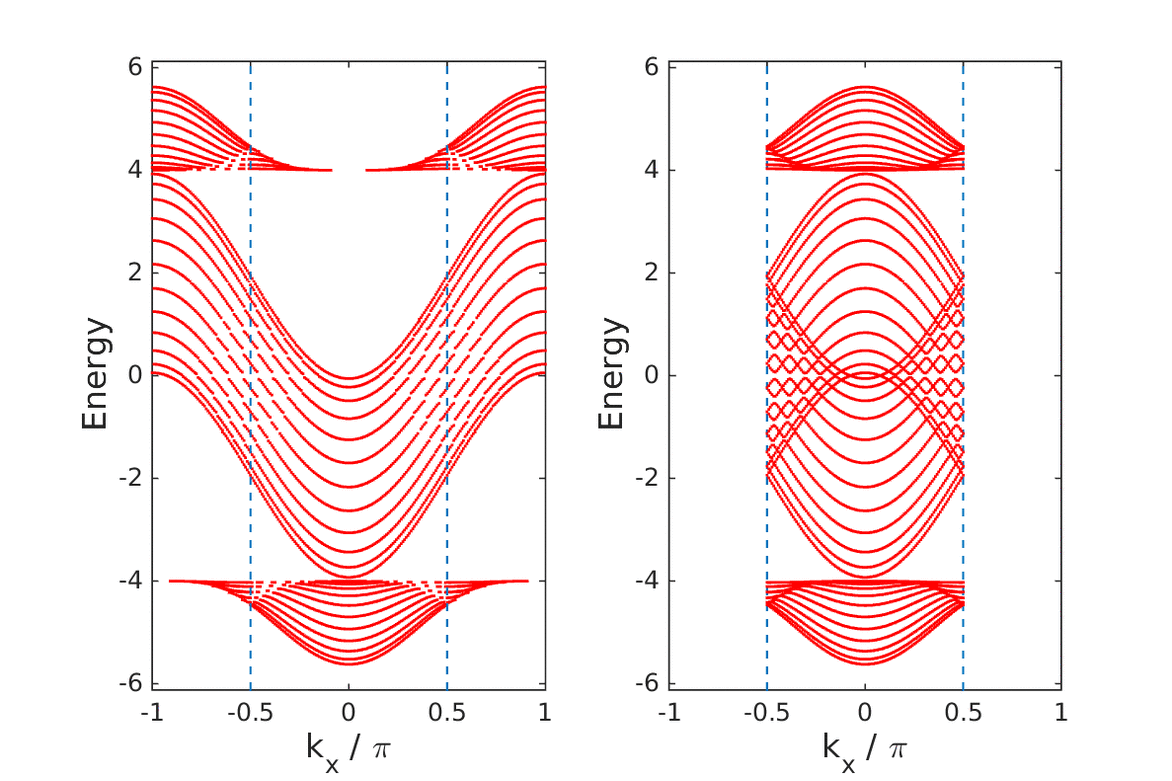 |
 |
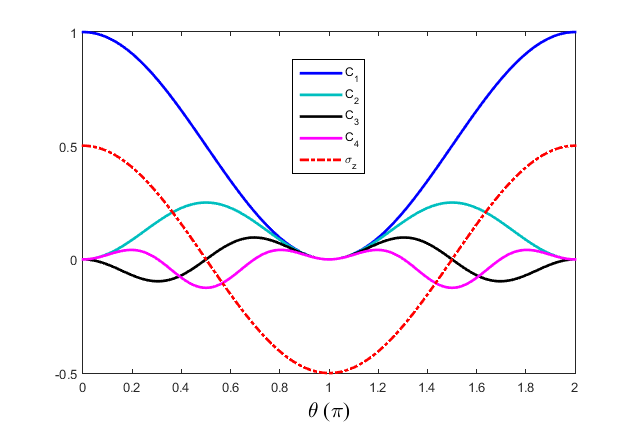
An expansion, similar to the cumulant expansion in probability theory, is carried out for the Bargmann invariant, which is the quantity from which the Berry phase can be derived. The derivation shows that the first term in the expansion corresponds to the Berry phase itself, the higher order terms can be interpreted as the associated cumulants; spread, skew, kurtosis, etc. The gauge invariance of all of these quantities is also demonstrated.
Cumulants of a spin-1/2 particle in a precessing field
|
|
 |